
Quand le cône … il sphère.
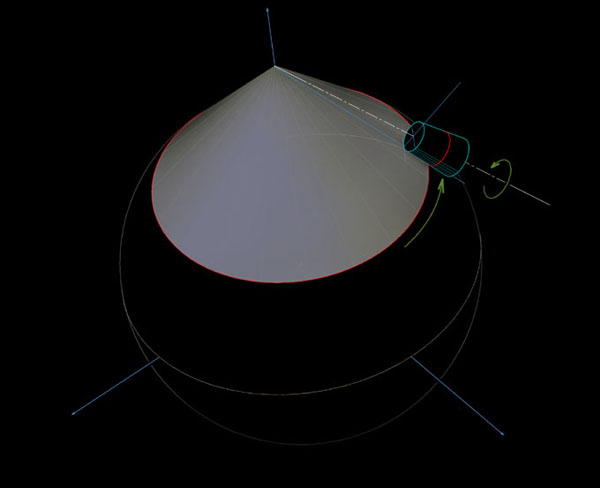
Sur ces images nous pouvons observer comment le dahu évolue sur une sphère. Sur l’image ci-dessous nous voyons comment nous pouvons faire apparaître un cône. Nous vous renvoyons aux numéros 21 et 22 pour saisir comment en décônant nous mettons à plat ce parallèle que dessine le dahu en circulant sur la sphère. Il existe une relation entre le rayon du cercle qui constitue le parallèle sur la sphère et le rayon de l’arc de cercle que nous obtenons sur la feuille plane en décônant.
Sur la sphère de rayon R le parallèle a un rayon r = R cos(l). ( l étant la latitude du parallèle (en radians)). Sur la feuille de papier sera imprimé un arc de cercle de rayon r’ = R / tang(l) et la part du « gâteau » (pour conserver l’image du numéro précédent) fera un angle a = 2p sin(l). Au passage vous pouvez vérifier que la longueur du parallèle est bien égale à la longueur de l’arc imprimé sur la feuille de papier.
Cette petite explication n’a pas d’autre intérêt, à ce stade, sinon vous montrer que la passage du monde sphérique au monde plat est possible, engendre des modifications mais qu’il est possible de traduire.
En positionnant le dahu * en différents parallèles nous obtiendrions une série de feuilles. Si vous tentiez de les rassembler en un livre ce serait bien difficile à relier : chacune aurait un rayon différent et une ouverture ou angle différent … quel drôle de volume cela vous ferait mais ça prendrait moins de place que la sphère si vous deviez conserver tout cela. D’autant moins que possédant la formule de traduction il vous suffirait de ne conserver sur une page que le rayon de la sphère et la formule **.
à suivre … mais dans deux ou trois semaines seulement, car des activités extérieures nous entraînent dans des salles obscures et que nos membres actifs nous rappellent qu’ils n’ont que deux bras et qu’ils ne s’appellent pas Shiva – Ca va … ça va on a compris. N’insistez pas. On ne vous demande pas d’avoir le don d’ubiquité déjà qu’il y a bien assez d’ambiguïtés.
Notes :
* question : Est-il possible d’employer le même dahu pour tous les parallèles ou bien doit on disposer de dahus différents pour chaque parallèle ?
** Ceci, en passant, vous permet de saisir pourquoi les fichiers images sont beaucoup moins lourds en « vectoriel » qu’en « pixellisation ». Dans le premier cas vous ne conservez que le nom de l’objet et la formule ( la caisse à outils) alors que dans le second cas il faut garder en mémoire tout l’ensemble des points qui constituent l’objet … il y en a une infinité si votre objet est continu mais en général comme on ne peut pas conserver une infinité … c’est la qualité de l’image ou de l’objet qui s’en ressent. Dans le premier cas vous voyagez léger mais à chaque pas vous devez refaire le calcul … mais quand on sait marcher il n’est pas difficile de mettre un pied devant l’autre sans trop se prendre la tête.
